Info
Snooker is a cue sport that originated in India in the latter half of the 19th century. The game is played on a rectangular table covered with green baize, with pockets at each of the four corners and in the middle of each long side. Players use a cue stick to pocket colored balls into the pockets, aiming to score points and outmaneuver their opponents. Snooker has become a popular and competitive sport worldwide, attracting enthusiasts from all walks of life.
For info, feedback and potential bugs: send me an email.
Tournament Draw
Below you will find all the tournament formats that my model supports (and a graphical representation of their respective expected outcome). For other formats please use the default (automatic) draw provided by cuescore.com.
For the fellow nerds
These specific formulae are intended to fix a few potential issues with the drawing of the cup-stages, for any sport, where there is prelimenary seeding and multiple qualifiers from groups. There are no alterations in this model for the group winners in any of the draw-formulae; they all still follow the principle of "highest seed meets lowest seed" - or equivalently: the principle of equal sum (i.e. for each round all the matches, assuming the expected result by seeding, will involve players whose seeding add up to the same number (e.g. in the quarter final stages: 1-8, 4-5, 3-6, 2-7 all up to 9)).
The only difference between the formats are the initial placement of the remaining qualifiers in the draw. The most prominent issue is that players from the same group should not be able to meet again before a potential final. We would of course like to chose an appropriate algorithm for the draw - and the main criteria should hence be the principle of "highest seed meets lowest seed" (see above), which obviously doesn't work because they (e.g. seed 1 and seed 16) will have played in the same group. This leaves, in general, a total of \( \big[ (\# \; of \; Qualifiers \, / \, 4)! \big] \) possible draws to choose from. The obvious next step is to place all the 2nd-place finishers by "mirroring" the draw of the 1st-place finishers (e.g. for 8 groups and 16 qualifiers: A1(1)-H2(15), B1(8)-G2(9), ... , H1(2)-A2(16)) ensuring that players from the same group end up in different halfs while also optimizing with regards to the principle of equal sum. This method works well enough, but there are some potential problems with it: if for example the 1st or 2nd seed have a slight slip-up in the group stages they will clash immediately in the first(!) knock-out match. One might argue that, in that case, it's deserved and the seeds shouldn't be over-protected - but after a trial of one year of this system it has been decided to try another, more elegant method (note: this method is also problematic because of the unfortunate fate of the 16th, 15th, 8th and 7th seed: you will see that these players will face tremendous and unreasonable difficulty in their efforts to climb up the rankings and improve their seeding).
Which brings us to the method in hand: the norwegian snooker community have decided to use a method for calculating the draw based on a principle I have dubbed "recursive mirroring" for the forseeable future. We wanted an elegant, mathematically rigorous model that didn't infringe on the fairness of the competition or seem unnaturally constructed - and among the many different possible paradigms of principle for the calculation of the draw - this is the method we landed on. As mentioned earlier, the draw for the group winners remains unchanged, while the 2nd-place finishers (where applicable) follow the principle of "mirroring" as described above. The 2nd place of the first group will meet the winner of the last group, the 2nd place of the second group will meet the winner of the penultimate group and so on. And now mirror the draw of the 2nd-place finishers again within each half of the draw, and then again by halving and mirroring again and continue recursively. Thus we have created a fair an elegant solution to the calculation of the draw for the knock-out stages - or at least laid the basis for a general principle to use as a guideline for the individual formats.
Note: as of 2026 a slight altercation of the "5 groups - 16 qualifiers"-draw has been agreed upon within the community. Please see the illustraition for details.
HC-rating
This model is an extension of the industry standard ELO-model for calculating playing strength and generating a rating list.The idea emanated from the need to evaluate the handicap (\(HC\)) between two players in the game of snooker. Fortunatly, we already have access to a rating list provided by the NBF (ELO-model with rating delta normalization factor 400 and \(K\)-factor 20) - from there it's just a matter of estimating a formula for calculating the \(HC\) based on the relative rating. This allows you the option of playing with, without or even with customized \(HC\) while maintaining the intergrity and true equilibrium of the model. Because of the intrinsic complexities of the game of snooker there is no rigorous way of determining this formula - hence I have tried to use my experience and knowledge to come up with an elegant solution:
$${ HC = HC_{max} (1 - e^{- ( | \Delta r | \, / \, \beta ) ^{\alpha}});}$$
where \( \Delta r =\) rating delta, \(HC_{max} = 147\), \( \alpha = 1\) and \(\beta = 1400\). The rating is updated upon completion of a match in accordance with the standard ELO-model using the formula:
$${ r = r_{0} + K (x - \bar{x}),}$$
where \(r_{0}\) is the old (current) rating, \(x\) is the normalized score, \(\bar{x}\) is the normalized expected score and \(K\) is a variable "\(K\)-factor". The expected score is calculated, as a function of the difference in rating (\(\Delta r\)), by:
$${\bar{x}_{A}(\Delta r) = \frac{1}{10^{- \Delta r \, / \, 400}}; \;\; \bar{x}_{B} = 1 -\bar{x}_{A}}$$
And \(K\) is decided by a number of factors: namely the robustness of both participating players, the distance of the match, the distance type and the selected "Update-Rating-System" (URS, see below):
$${K(d) = c_{\scriptsize D} \, c_{\scriptsize R} \, c_{\scriptsize{URS}} \, K_0 \Big[ 1 - e^{- \alpha d} + \beta \, d \, e^{- \epsilon (d-1)^2} \Big] ,}$$
where the variables and parameters are defined as follows:
- \( d : \) variable dependent upon "distance type"; equal to maximum distance (the number in the parenthesis of a match) for the "Best-of" option and equal to total frames played for "Free-frames".
- \( K_0 = 20 \) as defined above.
- \( c_{\scriptsize D} : \) coefficient dependent upon "distance type"; \( c_{\scriptsize D}= 0.8 \) for "Free-frames" and \( c_{\scriptsize D} = 1 \) for "Best-of".
- \(c_{\scriptsize R}\) is a coefficient of \(K\) arising from potential differences in robustness whose possible values are specified in table 1.
- \( \gamma \equiv 32/20 \) is a helpful constant we have introduced for notation.
- The remaining parameters are dependent upon which "URS" you choose and are defined in table 2.
Below you'll find a graph providing a visual representation of the difference in \( K(d) \) arising from which "URS"-option you choose ("by-frame" in blue and "by-match" in orange) and two tables defining parameters as stated above.
Figure 2: Graph of difference between URS
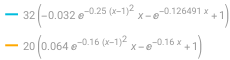
Table 1: Robustness coefficient
| A B | High |
Medium |
Low |
High |
11 | 0.751.5 | 0.53 |
Medium |
1.50.75 | 1.51.5 | 13 |
Low |
30.5 | 31 | 33 |
Table 2: URS-parameters
URS |
"By-match" |
"By-frame" |
\( c_{\scriptsize{URS}} \) |
\( 1 \) |
\( \gamma \) |
\( \alpha \) |
\( \gamma / 10 \) |
\( \sqrt{\gamma} / 10 \) |
\( \beta \) |
\( 4\gamma / 100 \) |
\( - 2 \gamma / 100 \) |
\( \epsilon \) |
\( \Big( \frac{1}{4 \gamma} \Big)^2 \) |
\( \Big( \frac{1}{2} \Big)^2 \) |
How To Apply
Hopefully the interface is pretty self explanetary, however there are a few things you should note - particularly perteining to the match protocol:
- You can't edit a match after it is finished.
- Positive HC means player B starts with extra points and negative HC means player A gets a head start. Denoted by number of points granted at the start of each frame, in parenthesis, behind the player's name in the match display.
- Please consider your spelling carefully when typing out player names (or, preferably, use the autocompletion).
- When creating a new match you can choose whether to play a specific distance (best-of) or just playing a non-specified number of frames (free-frames) where you can end the match whenever it suits you.
- Please note that matches of longer distances weigh slightly heavier when updating rating.
- Update-rating-by-system (URS) refers to whether you want, opun completion of match, to update rating by match outcome (win-lose-draw) or by frame score (i.e. a match finished 4-3 when the expected outcome was closer to 4-2 will actually result in an increase of the losing player's rating - like in chess); the "frames"-option weighs slightly heavier than the "match"-option for longer matches, but will usually result in fewer points.
- Update the score and other parameters of a match by clicking the "edit"-button (which you can find within the expandable part of the match display).
- Should there be a need for manual correction due to an error please contact me directly (as above).